O Poder da Álgebra Linear em Aprendizado de Máquina

Visão Geral da Aula

Nesta aula, você explorará os conceitos fundamentais da álgebra linear, focando em suas aplicações no aprendizado de máquina. Você entenderá por que dominar este campo é crucial para desenvolver algoritmos eficientes e descobrir relações ocultas dentro dos dados. Através de atividades, um estudo de caso real e um laboratório, você ganhará experiência prática na aplicação de técnicas de álgebra linear para resolver problemas complexos.

Objetivos de Aprendizagem

Ao final desta aula, você será capaz de:

1. Compreender os conceitos fundamentais de álgebra linear e sua importância no aprendizado de máquina.
2. Aplicar técnicas de álgebra linear para calcular sistemas complexos de maneira eficiente.
3. Utilizar vetores para representar dados e realizar operações básicas.
4. Reconhecer o poder da abstração na álgebra linear para estimular a criatividade e a inovação.

Conteúdo da Aula

Introdução à Álgebra Linear

• Definição e importância no aprendizado de máquina.
• O papel da álgebra linear na computação mais rápida e na extração de relações de dados.
• Reflexão pessoal sobre a beleza e abstração da matemática.

Os Fundamentos: Vetores

• Definição de um vetor.
• Operações básicas com vetores: adição, subtração e multiplicação por escalar.
• Visualização de vetores em diferentes dimensões.

Aplicações no Aprendizado de Máquina

• Como os algoritmos de álgebra linear aprimoram a IA.
• Exemplos de algoritmos de aprendizado de máquina que dependem da álgebra linear.

Abstração em Álgebra Linear

• A beleza e o poder da abstração matemática.
• Como a abstração pode simplificar problemas complexos..

Aplicações Práticas em Aprendizado de Máquina

• Algoritmos de aprendizado de máquina que dependem de álgebra linear.
• Exemplos concretos de uso em inteligência artificial.

Atividades

1. Prática de Manipulação de Vetores.

Para praticar a manipulação de vetores, vamos seguir os passos abaixo:

1. Definição dos vetores:

   • Comece definindo alguns vetores em um espaço 2D ou 3D.

2. Operações básicas:

   • Adição de vetores:                  a+b
   • Subtração de vetores:           a−b
   • Multiplicação por escalar:  k⋅a

3. Visualização dos vetores:

   • Usaremos uma ferramenta de gráficos, como o Matplotlib no Python, para visualizar os vetores.

Passo 1: Definição dos Vetores

Vamos definir dois vetores em um espaço 2D:

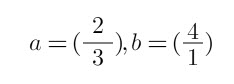
Passo 2: Realização das Operações Básicas

Adição de Vetores

A adição de vetores é um conceito importante na matemática que é muito útil em várias áreas, como física e engenharia. Para explicar a adição de vetores, imagine que um vetor é como uma seta que aponta para uma direção específica e tem um certo comprimento.

Quando você adiciona dois vetores, você está basicamente combinando as direções e os comprimentos das setas. Para fazer isso, você coloca a ponta de uma seta na base da outra. O vetor resultante, chamado de vetor soma, vai da base da primeira seta até a ponta da segunda seta. Isso é como desenhar um caminho que começa no ponto inicial de um vetor e termina no ponto final do outro vetor.

Vamos pensar em um exemplo simples para facilitar a compreensão. Suponha que você tem dois vetores em um plano. O primeiro vetor pode ser uma seta que vai de um ponto A para um ponto B. O segundo vetor é outra seta que vai do ponto B para um ponto C. Quando você adiciona esses vetores, você está simplesmente conectando o ponto A diretamente ao ponto C com uma nova seta, que representa a soma dos dois vetores originais.

Em termos matemáticos, a adição de vetores é feita somando as suas componentes. Por exemplo, se o primeiro vetor tem uma componente horizontal de 3 unidades e uma componente vertical de 4 unidades, e o segundo vetor tem uma componente horizontal de 1 unidade e uma componente vertical de 2 unidades, a soma desses vetores terá uma componente horizontal total de 4 unidades (3 + 1) e uma componente vertical total de 6 unidades (4 + 2).

Portanto, a adição de vetores é uma maneira de combinar direções e magnitudes para obter um vetor que representa a soma dos vetores originais. Isso ajuda a visualizar e resolver problemas onde várias direções e forças estão envolvidas.

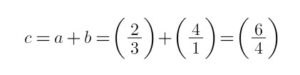
Subtração de Vetores

Vector subtraction is another essential concept in vector algebra. Similar to vector addition, it involves combining vectors, but instead of adding their magnitudes and directions, you are finding the difference between them. This process can be visualized and understood through a few basic steps.

Imagine you have two vectors, represented by arrows, on a piece of paper. Let’s call them $\mathbf{a}$ and $\mathbf{b}$. Vector subtraction involves determining the vector that, when added to $\mathbf{b}$, gives you $\mathbf{a}$. This is done by reversing the direction of vector $\mathbf{b}$ and then adding it to $\mathbf{a}$. The resultant vector represents the difference between the two vectors.

Mathematically, if you have vectors   and ,

the subtraction is performed by subtracting the corresponding components of b from a. This gives you a new vector c where . For example, if   and , the difference

To visualize this, place the tail of vector $\mathbf{b}$ at the head of vector $\mathbf{a}$, but in the opposite direction (since it’s subtracted). The arrow pointing from the tail of $\mathbf{a}$ to the head of the reversed $\mathbf{b}$ gives you the resultant vector. This new vector represents how much you need to adjust vector $\mathbf{b}$ to reach vector $\mathbf{a}$.

Understanding vector subtraction is crucial in many applications, such as physics, where it can represent differences in position, force, or velocity. For example, if you are tracking the movement of an object, subtracting its initial position vector from its final position vector gives you the displacement vector, showing the overall change in position. This method helps to analyze and solve problems involving relative motion and other vector-related phenomena.

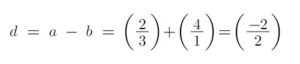
Multiplicação por Escalar

Multiplication by a scalar is a basic but powerful operation in vector algebra. It involves scaling a vector, which means adjusting its length without changing its direction. This concept can be understood through a few simple steps and visualizations.

Imagine you have a vector represented by an arrow on a piece of paper. This vector has both a direction and a magnitude (length). When you multiply this vector by a scalar (a single number), you are scaling the vector’s length while keeping its direction the same. A scalar is just a real number, such as 2, -1, or 0.5.

To visualize scalar multiplication, imagine you have a vector $\mathbf{a}$ with a certain length and direction. If you multiply $\mathbf{a}$ by a scalar $k$, the resulting vector will have the same direction as $\mathbf{a}$, but its length will be scaled by the factor $k$. For example, if you multiply $\mathbf{a}$ by a scalar of 2, the length of the vector will double, but the direction will remain unchanged. Conversely, multiplying by a scalar of 0.5 will reduce the vector’s length to half of its original size.

Mathematically, if you have a vector a=(a1,a2)mathbf{a} = (a_1, a_2)a=(a1​,a2​) and you multiply it by a scalar $k$, the result is a new vector k⋅a=(k⋅a1,k⋅a2)k cdot mathbf{a} = (k cdot a_1, k cdot a_2)k⋅a=(k⋅a1​,k⋅a2​). For example, if $\mathbf{a}=(3,4)$ and you multiply it by 3, the result is $3\cdot \mathbf{a}=(3\cdot 3,3\cdot 4)=(9,12)$. If you multiply the same vector $\mathbf{a}$ by -1, the result is $-1\cdot \mathbf{a}=(-3,-4)$, which not only scales the vector but also reverses its direction.

Scalar multiplication is used in various applications, such as adjusting the magnitude of vectors in computer graphics, physics simulations, and more. It helps in understanding how changes in scale affect vectors and in manipulating vectors to achieve desired results in different fields. This operation is fundamental to many concepts in linear algebra and helps build a deeper understanding of vector behavior and manipulation.

Vamos multiplicar $\mathbf{a}$ por um escalar $k=2$:

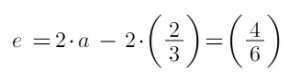
Passo 3: Visualização dos Vetores

Agora, vamos visualizar os vetores resultantes usando o Matplotlib.

import matplotlib.pyplot as plt 
import numpy as np 

# Definir os vetores 
a = np.array([2, 3]) 
b = np.array([4, 1]) 
c = a + b 
d = a - b 
e = 2 * a 

# Configurar o gráfico 
plt.figure() 
plt.quiver(0, 0, a[0], a[1], angles='xy', scale_units='xy', scale=1, color='r', label='a') 
plt.quiver(0, 0, b[0], b[1], angles='xy', scale_units='xy', scale=1, color='g', label='b') 
plt.quiver(0, 0, c[0], c[1], angles='xy', scale_units='xy', scale=1, color='b', label='a + b')
plt.quiver(0, 0, d[0], d[1], angles='xy', scale_units='xy', scale=1, color='y', label='a - b')
plt.quiver(0, 0, e[0], e[1], angles='xy', scale_units='xy', scale=1, color='m', label='2 * a') 

# Ajustar limites do gráfico 
plt.xlim(-5, 7) 
plt.ylim(-1, 7) 

# Adicionar grade e legenda 
plt.grid() plt.legend() 

# Mostrar o gráfico 
plt.show()

1. 1. Definição dos Vetores: Utilizamos numpy para definir os vetores $\mathbf{a}$ e $\mathbf{b}$.
   2. Operações: Calculamos os vetores resultantes das operações de adição, subtração e multiplicação por escalar.
   3. Visualização: Utilizamos a função quiver do Matplotlib para desenhar os vetores em um gráfico 2D, com cores diferentes para cada operação. Configuramos os limites do gráfico, adicionamos uma grade e uma legenda para facilitar a visualização e entendimento dos vetores.

Este exercício é uma ótima prática para entender como as operações básicas em vetores funcionam e como visualizá-las, facilitando a compreensão dos conceitos de álgebra linear.

Exploração da Abstração

• • Refletir sobre um problema complexo em sua vida diária ou estudos e descrever como a abstração poderia ajudar a simplificá-lo.
  • Discutir com colegas ou escrever um breve ensaio sobre como a álgebra linear pode ser usada para abstrair e resolver este problema.

Exploração de Conceitos

• • Refletir sobre um problema complexo em sua vida e descrever como a abstração poderia ajudar a simplificá-lo.
  • Discussão em grupo ou ensaio curto sobre a aplicação da álgebra linear para resolver este problema.

Prática de Operações Básicas

• • Realizar operações básicas (adição, subtração, multiplicação por escalar) em vetores fornecidos.
  • Visualizar os resultados usando ferramentas gráficas.