Introdução à Matemática Linear

What Is a Vector?

You can think of a vector in simple terms as a list of numbers where the position of each item in this structure matters. In machine learning, this will often be the case. For example, if you are analysing the height and weight of a class of students, in this domain, a two-dimensional vector will represent each student:

( ) ( ) v1 1.64 −→v = ( v ) = ( 64 ) 2

Here v₁ represents the height of a student, and v₂ represents the weight of the same individual. Conventionally, if you were to define another vector for a different student, the position of the magnitudes should be the same. So the first element is height, followed by weight. This way of looking at vectors is often called the “computer science definition”. I am not sure if that is accurate, but it is certainly a way to utilise a vector. Another way to interpret these elements that is more relevant to linear algebra is to think of a vector as an arrow with a direction dictated by its coordinates. It will have its starting point at the origin: the point (0, 0) in a coordinate system, such as the x,y plane. Then the numbers in the parentheses will be the vector coordinates, indicating where the arrow lands:

xy−123−123−→v 11

Figure 3.1: An example of a vector.

Figure 3.1 represents a visual interpretation of the vector −→ v :

( ) −→ 2 v = ( 3)

As you can see, we moved from the base, point (0, 0), by two units to the right on the x axis and then by three units to the top on the y axis. Every pair of numbers gives you one and only one vector. We use the word pair here as we are only working with two dimensions, and the reason for using this number of coordinates is to create visual representations. However, vectors can have as many coordinates as needed. For example, if we wish to have a vector −→t within a three-dimensional space, we could represent it using a triplet. There is no limitation to the dimensions a vector can have:

( ) 2 −→ || 3|| t = ( ) 5

In my opinion, the best way to understand linear algebra is by visualising concepts that, although simple but powerful, are often not well-understood. It is also essential to embrace abstraction, and let ourselves dive into definitions by bearing this concept in mind, as mathematics is a science of such notions. The more you try to understand abstract concepts, the better you will get at using them. It is like everything else in life. So bear with me as I introduce the first abstract definition of the book: a vector is an object that has both a direction and a magnitude:

M−→DOavirgrinegicittnuidoen

Figure 3.2: The components of a vector.

Alright, let’s try and break this concept down, starting with direction. We know that a vector has a starting point, which we call the base or origin. This orientation is dependent on a set of coordinates that in itself is essential for defining this element. For example, look at the figure above. The landing point defines the direction of the vector −→ v . Magnitude is the size of the vector, and it is also a function of where it lands. Therefore, for two vectors to be the same, their directions and magnitudes must be equal. Now that we have a visual interpretation and an abstract definition, the only thing missing when it comes to fully understanding vectors is a context, a real-life situation where they are applicable. Providing context will indicate where this can be utilised and make the understanding of such notions more accessible. For example, say that you need to describe the wind. How many information points do you need to understand the wind if you want to sail? Well, I believe that two points of information will generally be sufficient. You will certainly need the wind direction and the speed, and one vector can represent this well. If directions and magnitudes define vectors, it would be advantageous to apply mathematical operations to them; one example could be to describe paths. If we break down one course into two vectors, perhaps we could represent it as a sum of such elements.

Vectors alone are instrumental mathematical elements. However, because we define them with magnitude and directions, they can represent many things, such as gravity, velocity, acceleration, and paths. So let’s hold hands and carefully make an assumption. We know nothing more about linear algebra yet, but there is a need to move on, well at least for me there is, before you call me a thief, as so far I have charged you money just for a drawing of an arrow. If we only know how to define vectors, one way to carry on moving forward will maybe be to try to combine them. We are dealing with mathematics, so let’s try to add them up. But, will this make sense? Let’s check.

3.1 Is That a Newborn? Vector Addition

Given two vectors −→ v and −→ w we can define their sum, + as a translation from the edge of −→v with the magnitude and direction of . Did you shit yourself with all the mathematical terms? Well, there’s nothing to worry about. There are two positives about that accident:

You can go to a party and try to impress someone with the phrase ”translation from the edge of where one vector finishes of the magnitude and direction of the other one”; however, I will warn you that if somebody really is impressed by that… well take your own conclusions.
This is another step into the world of abstraction, and a visual explanation will follow.

Let’s see what is happening here. First, let’s consider two vectors: −→ v and −→ w , which will be defined by the following pairs of coordinates:

( ) ( ) 2 2 −→v = ( 3) , −→w = ( 1 )

If we make use of the Cartesian plane and plot these vectors, we will have something like this:

−→−→ xy−123−123wv11

Figure 3.3: The representation of two vectors.

We want to understand geometrically what happens when we add two vectors:

−→v + −→w

Considering that directions and magnitudes define vectors, what would you say if you had to take a naive guess at the result of adding two vectors together? In theory, it should be another vector, but with what direction and magnitude? If I travel in the direction of −→v to its full extent and then turn to the direction that −→ w points and go as far as its magnitude, I will arrive at a new location. The line from the origin to the new location where I landed, is the new vector −→ v + . Let’s take a pause here and analyse what just happened. Mathematics is a science developed by people, so do not become discouraged by a formula. Don’t just read it, think that you can’t understand it, or pretend that you did and move on. Question it!

Analytically this is how you would do this operation:

−→ −→ −→ z = v + w

( ) ( ) −→ 2 2 z = ( 3 ) + ( 1)

The vector −→z is the result of adding the elements with the same positions in vectors −→ v and −→ w :

( ) ( ) −→ 2 + 2 4 z = ( 3 + 1) = ( 4)

We can explore a visualization to understand these so-called translations better and solidify this concept of vector addition:

xy−1234−1234−→−→w−→vv11+ −→w

Figure 3.4: The addition of two vectors.

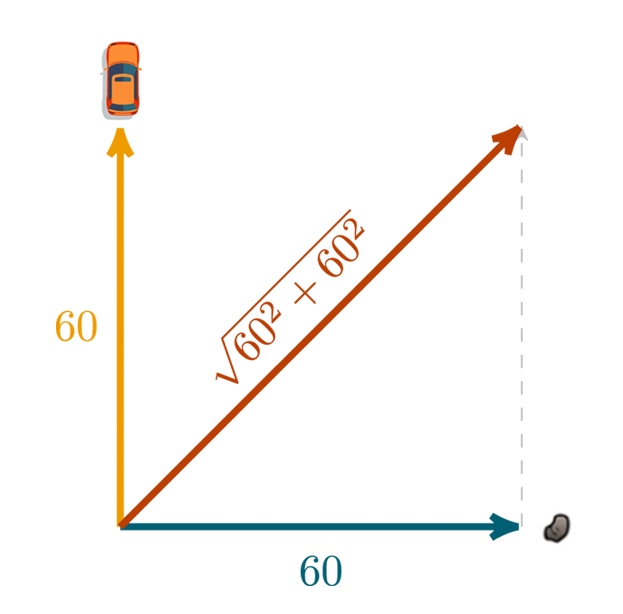
One can utilize vector addition in many real-life scenarios. For example, my cousin has a kid with these long arms who can throw a golf ball at 60 km/h:

Figure 3.5: My cousin’s kid

One day we were driving a car north at 60 km/h. From the back seat, he threw this golf ball through the window directly to the east. If we want to comprehend the direction and velocity of the ball relative to the ground, we can use vector addition. From vector addition, we can understand that the ball will be moving north-east, and, if you wished to calculate the velocity, you could do so by using the Pythagoras theorem, √ ---2------2 60 + 60 . It is an elementary example, and the wind resistance was ignored:

√-------- 6600602 +602

Figure 3.6: My cousin’s kid rock throw.

Well, if you can add vectors, it will also be possible to subtract them. It will be the same as if you were to find the sum of two vectors, but instead of going outward in the direction of the second vector, you will go the other way. There is another thing that one can do with a vector. We can change its magnitude and direction. To do so, we can multiply it by a scalar, a number that will stretch or shrink it.

3.2 Wait, Is That Vector on Steroids? Scalar Multiplication

A scalar can be any real number. If you don’t recall the definition of a real number, I can refresh your memory, but what happened along the way? A real number is any number you can think of. Are you thinking about a number that seems mind blowing complicated , like π? Yeah, that is a real number. Analytically we can define a real number thus:

λ ∈ ℝ

The λ is a variable or a scalar that can accommodate any real number. The other new symbol, ∈, means to belong to something; that something here is the set of real numbers, which we symbolise as ℝ. As λ is a real number, there are four different outcomes when multiplying a vector by a scalar. First, we can maintain or reverse the vector’s direction depending on this scalar’s sign. Another thing that will be altered is the length of the vector. If λ is between 0 and 1, the vectors will shrink, whereas if the value of λ is greater than 1 or -1, the vector will stretch:

If λ > 1 the vector will keep the same direction but stretch.
If 1 > λ > 0 the vector will keep the same direction but shrink.

A couple more cases:

If λ < −1 the vector will change direction and stretch.
If 0 > λ > −1 the vector will change direction and shrink.

Symbolically, multiplying a vector −→ v by a scalar λ can be defined by:

−→ λ v

If we define a new vector −→g such that:

−→g = λ −→v and λ = − 2

It follows:

( ) −→ 2 g = − 2 ⋅( 3)

Finally:

( ) − 4 −→ ( − 6) g =

Because we defined λ to be -2, the result of multiplying the vector −→ v by this scalar will be a stretched version of the same −→v but pointing to a different direction. In figure 3.7, we can see a visual representation of this operation:

xy−−−−−−123456−−−−−123456−→v−→g 65432165432

Figure 3.7: The multiplication of a vector by a scalar.

We are now at a stage where we know how to operate vectors with additions and subtractions, plus we are also capable of scaling them via multiplication with a real number. What we still haven’t covered is vector multiplication.

3.3 Where Are You Looking, Vector? The Dot Product

One way that we can multiply vectors is called the dot product, which we will cover now. The other is called the cross product, which won’t be covered in this book. The main difference between the dot product and the cross product is the result: the dot product result is a scalar, and what comes from the cross product is another vector. So, suppose you have two vectors of the same dimension. Then, taking the dot product between them means you will pair up the element entries from both vectors by their position, multiply them together, and add up the result of these multiplications.

So, for example, consider the vectors:

( ) ( ) 2 2 −→v = ( 3) ,−→w = ( 1)

We can then calculate the dot product between −→ v and −→ w as such:

( ) ( ) 2 2 −→v ⋅ −→w = ( 3) ⋅( 1) = 2 ⋅ 2 + 3 ⋅ 1 = 7

A definition for this same concept given any two vectors, −→ v and −→ w where each of them have n elements, which is the same as saying that the vectors are of size n is:

−→ −→ ∑ n v ⋅ w = vi ⋅ wi i=1

(3.1)

One of the goals of this series of books is for you to become comfortable with notation. I believe it will be of great value; therefore, I will describe each symbol introduced throughout the series. For example, the symbol ∑ is the capital Greek letter sigma; in mathematics, we use it to describe a summation, so:

∑n vi ⋅ wi = v1 ⋅ w1 + v2 ⋅ w2 + ...+ vn ⋅ wn i=1

In essence, we have an argument with an index, v_iw_i, representing what we are going to sum. Now the numbers above and below the sigma will be the controlling factors for this same index that is represented by the letter i. The number below indicates where it starts, whereas the number above is where it needs to end. In the example above, we have two components per vector and need them all for the dot product, so we have to start at one and end at two, meaning that i = 1 and n = 2.

I learned the dot product just like that. I knew I had to perform some multiplications and additions, but I couldn’t understand what was happening. It was simple, and because I thought that computing it was enough, this led me to deceive myself into thinking that I fully understood it. I paid the price later, when I needed to implement these concepts to develop algorithms. The lack of context and visualisation were a killer for me.

A true understanding of linear algebra becomes more accessible with visualisations, and the dot product has a tremendous geometrical interpretation. It can be calculated by projecting the vector −→ w into −→ v and multiplying the magnitude of this projection with the length of −→v , or vice versa. In other words, the dot product will represent how much of −→w points in the same direction as −→v . Let’s verify this; so, given the vectors and , a projection of −→ w into −→ v can be represented this way:

−→−→ xy−123−123𝜃vw 11

Figure 3.8: The angle between two vectors.

Projections are a fundamental concept in machine learning, particularly in understanding how data can be represented in lower-dimensional spaces. They can be intuitively understood by considering angles and movement in the context of vectors.

Imagine two vectors, say −→v and −→w , originating from the same point (or having the same base). Let 𝜃 be the angle between these two vectors. This angle measures the deviation of one vector from the other in terms of direction. However, the idea of ”moving one of these vectors by 𝜃 degrees to end up on top of the other” needs clarification. In the context of vector projections, what we’re actually doing is projecting one vector onto another. This projection is not about rotating the vector but rather about finding the component of one vector that lies along the direction of the other vector.

The projection of vector −→w onto vector −→v is a new vector that lies on the line of −→ v and represents the component of −→ w in the direction of :

−→−→ xy−123−123vw 11proj

Figure 3.9: The projection of −→w

into

If we are after a number representing how much a vector points in the direction of another, it makes sense for us to use their lengths. Therefore, we need to calculate two measures: the length of −→ v and the length of the projection of −→ w into . We already know how to calculate the length of −→v , and the norm of the projection of −→w into −→v can be derived using the Pythagorean theorem. Given a vector’s elements (the coordinates), we can quickly draw a triangle. Let’s take −→v , the vector for which we need the magnitude:

−→−→ w𝜃v

Figure 3.10: Square triangle.

So, we know that the square of the hypotenuse is equal to the sum of the squares of the cathetus (we should, right?). Generically, we can represent the vector −→ v as = (v₁,v₂)^T, where v₁ and v₂ can take for values any real number. The vector has been working for a long time. It is an active presence throughout math books. But, like all of us, is ageing, and its knees are not like they used to be. So the T means that −→v can lie down for a moment, or in other words, it becomes transposed. Therefore T stands for a transposed version of the element in question, where columns become rows and rows become columns. We have been talking about lengths so it is about time we come up with a way of calculating such thing:

−→ ((v02,,03 ))

Figure 3.11: The length of a vector.

When we defined vectors, we established that the landing point was essential to describe the magnitude of such elements. If we have two points, the basis of the vector and the point on which the vector lands, we can use the formula to calculate the distance between two points to derive the length of this mathematical concept. It comes that we can calculate this distance with the following equation:

∘ --------------------------- (x − x )2 + (y − y )2 1 2 1 2

Where the x’s and the y’s represent the point’s coordinates, if we now use the coordinates of the landing point and the origin to calculate the distance between these two points, we will have something like this:

∘ ---------------------- (2 − 0)2 + (3 − 0 )2

Which in turn:

∘ ------------- (2)2 + (3)2

Because all vectors have the same origin, the point (0, 0), the length of −→ v is then equal to:

−→ ∘ ------------------------ ∥ v ∥ = (v1 − 0)2 + (v2 − 0 )2

Where v₁ and v₂ are generic coordinates for a landing point.

--------- −→ ∘ ∥ v ∥ = v21 + v22

Which gives us:

∘ --------- −→ 2 2 √ --- ∥ v ∥ = 2 + 3 = 13

This metric can also be called the “norm” of a vector; to be rigorous, as we should be, this norm is called the Euclidean norm. The fact that there is a name for a specific norm suggests that there are more of them in mathematics, which is exactly right. There are several definitions for norms, and each of these is calculated with a different formula. We will use the Euclidean norm for most of this book.

What if we are in a higher dimensional space, will this norm scale? The answer is yes, and we can get to the formula by using the same equation for the distance between points. So, let’s try and calculate it for three dimensions, then see if we can extrapolate for n dimensions. The problem is that we are stuck with a formula that takes only two components. There are paradoxes in mathematics. Some are problems that are yet to be proven, and some are just curiosities. This one is spectacular; mathematicians do not like to do the same thing several times, so the ideal situation is to work for one case and then generalize for all. The goal is to save time so that, at the next juncture, when a similar problem arises, we have a formula that can solve it, which is an astonishing idea on paper. The funny bit is that sometimes it takes a lifetime to find the equation for the general case.

So for the next 200 pages, we will be… calm down, this one will be quite simple. So, (v₁,v₂,v₃)^T can represent any vector with three coordinates. Let’s use it and try to derive a generic equation for the norm formula. As it stands now, if we only consider what we have learned in this book, we can’t say that we are at Einstein’s level of intellect, YET! Gladly for this particular case we can get ourselves out of trouble easily:

∘ -------------------------------------- ∥−→v ∥ = (v1 − 0)2 + (v2 − 0)2 + (v3 − 0)2

So it comes that:

∘ -------------- ∥ −→v ∥ = v21 + v22 + v23

Generically the norm of a vector with n components can be calculated with the following equation:

┌ ------- │ n −→ │ ∑ 2 ∥ v ∥ = ∘ vi i=1

I know this is a simple concept with a rudimentary formula, but formulas can be deceiving. Sometimes, we see them, assume that they are true, move on, and think that it is understood. The problem here is that while you can just choose to trust religion, don’t just trust science. Criticise it. The more you do this, the more you will learn. Blindly relying on everything that you are shown will appeal to the lazy brain as it removes the necessity to think about things. We can’t forget why we did all that: the dot product! Yet another magnitude has to be calculated, but this time it is of the projection of −→ w into −→ v . For this, we will again use trigonometry. Yes, that word that everybody was afraid of in High School. Someone must have placed a negative connotation on that word, and I suspect it was similar to the way they handled potatoes. All of a sudden, two or three fitness blogs claim that potatoes are evil, and there you go, you can only eat sweet potatoes, or better, sweet potato fries, which are certainly much better for you than regular boiled potatoes. Figure 3.10 has a representation of a squared triangle with an angle of size 𝜃. With the Pythagorean theorem, we can express the length of the projection of −→w as a function of the length −→w and the angle 𝜃:

−→−→−−−−→→ ww𝜃∥vprwoj∥.cos (𝜃 )

Figure 3.12: The length of the projection of −→ w

into

Okay, so after all of this, we have a geometrical approach to the derivation of the dot product for two vectors −→v and −→w which is:

−→ −→ −→ −→ v ⋅ w = ∥ v ∥ ⋅ ∥ w ∥ ⋅ cos 𝜃

(3.2)

We know from previous calculations that −→ v ⋅ −→ w = 7. We did this when we introduced the dot product; let’s verify if we get the same result with this new formula. For that, we need 𝜃, but don’t worry, I calculated it already, and it comes to around 29.4 degrees. Let’s compute this bastard then:

√ --- ∥−→v ∥ = 13

The norm of −→ w has the same value:

−→ √ -- ∥w ∥ = 5

Consequently:

−→ −→ √ --- √ -- ∥ v ∥ ⋅ ∥w ∥ ⋅ cos 𝜃 = 13 ⋅ 5 ⋅ cos(29.4 ) = 7

The dot product tells you what amount of one vector goes in the direction of another (thus, it’s a scalar ) and hence does not have any direction. We can have three different cases:

The dot product is positive, ⋅ > 0, which means that the two vectors point in the same direction.
The dot product is 0, ⋅ = 0 , which means that the two vectors are perpendicular, the angle is 90 degrees.
The dot product is negative ⋅ < 0 , which means that the vectors point in different directions.

This may still be a bit abstract—norms, vectors, and how they align with each other’s directions, so let’s explore an example. Imagine we are running a streaming service where movies are represented by 2-dimensional vectors. Although this is a simplified representation, it helps us understand the applications of the dot product. In our model, each entry of our vectors represents two genres: drama and comedy. The higher the value of an entry, the more characteristics of that genre the movie has.

Our task is to recommend a movie to a user, let’s call her Susan. We know that Susan has watched movie −→ a , represented by:

( ) −→ 1 a = 3

In our library, we have two more movies that we could recommend to Susan, movies −→b and −→c :

( ) ( ) −→ 4 −→ 2 b = , c = 2 3

Let’s visualize these movie vectors :

−→−→−→ xy−123−123abc 11

Figure 3.13: What should we recommend to Susan?

Given that we have information on Susan’s movie preferences, specifically her liking for the movie represented by vector −→a , our mission is to figure out which among the other two contenders, −→b and −→ c , we should recommend. It is no secret that using the dot product will make sense; this is the example for its applications, but why? The dot product between two vectors essentially measures how much one vector aligns with the direction of the other. A higher dot product indicates a greater level of similarity. Thus, by comparing the dot products of −→ a with both −→ b and −→ c , we can discern which movie aligns more closely with Susan’s preferences. The movie corresponding to the vector with the highest dot product emerges as the most similar to −→a , the most likely candidate for recommendation. However, we’ve already established how to calculate the dot product, so why don’t we take the opportunity to explore another widely used method in machine learning? One that builds on this same concept is the cosine similarity.

Recall that the dot product is expressed by 3.2, where 𝜃 is the angle between vectors −→v and −→w . Cosine similarity focuses on this cos(𝜃) term, revealing how vectors are oriented concerning each other. To compute cosine similarity, we rearrange the dot product formula to isolate cos(𝜃):

−→ −→ cos 𝜃 = ---v--⋅w----- −→ −→ ∥ v ∥ ⋅ ∥ w ∥

(3.3)

We have a phew things to compute. Let’s start with the norms:

∘ --------- √ ------ √ --- ∥ −→a ∥ = 12 + 32 = 1 + 9 = 10

−→ ∘ --------- √ -------- √ --- ∥ b ∥ = 42 + 22 = 16 + 4 = 20

∘ --------- √ ------ √ --- ∥ −→c ∥ = 22 + 32 = 4 + 9 = 13

There we go! We are just missing two dot products:

a ⋅ b = 1 ⋅ 4 + 3 ⋅ 2 = 4 + 6 = 10

a ⋅ c = 1 ⋅ 2 + 3 ⋅ 3 = 2 + 9 = 11

Now for the cosines:

−→ −→ ---a--⋅-b---- ----10------ -10---- cos (𝜃)a,b = −→ = √ --- √ ---= √ -----≈ 0.707 ∥−→a ∥ ⋅ ∥ b ∥ 10 ⋅ 20 200

−→ −→ cos (𝜃) = ---a--⋅-c----= √---11√-----= √11----≈ 0.964 a,c −→ −→ 10 ⋅ 13 130 ∥ a ∥ ⋅ ∥ c ∥

After calculating the cosines, we observe that its value between −→ a and −→ b is approximately 0.707, while the other cosine between and −→ c is approximately 0.964. It’s essential to understand the behavior of the cosine in this context: this function ranges from −1 to 1, where 1 indicates that the vectors are perfectly aligned (pointing in the same direction), 0 shows orthogonality (no similarity), and −1 means that the vectors are opposed. In our case, a higher cosine value signifies greater similarity. Therefore, the movie represented by vector −→ c , with a cosine of 0.964 concerning Susan’s watched movie −→a , shows a higher degree of similarity compared to the movie represented by vector −→ b , which has a cosine of 0.707. This implies that shares more characteristics with Susan’s preferred genres, so please enjoy your evening with movie −→ c . Visually, we could observe this result as this is a straightforward example. If both methods were applicable here, meaning we could have used the dot product or the cosine similarity, which one should we pick?

The choice between using the dot product and cosine similarity depends on the specific goals of your analysis. Use the dot product when the magnitude of vectors is crucial, as it provides a measure that combines both direction and magnitude. In contrast, opt for cosine similarity when you’re interested in comparing the direction or orientation of vectors regardless of their size. This makes cosine similarity ideal for applications like text analysis or similarity measurements in machine learning, where the relative orientation of vectors is more important than their length.

So, we now have a few ways to manipulate vectors. With this comes power and consequently, responsibility, because we need to keep these bad boys within certain limits.

3.4 A Simpler Version of the Universe – The Vector Space

In linear algebra, a vector space is a fundamental concept that provides a formal framework for the study and manipulation of vectors. Vectors are entities that can be added together and multiplied by scalars (numbers from a given field such as ℝ), and vector spaces are the settings where these operations take place in a structured and consistent manner.

A vector space can be thought of as a structured set, where this set is not just a random collection of objects but a carefully defined group of entities, known as vectors, which adhere to specific rules. In mathematical terms, a vector space is a set equipped with two operations, forming a triple (O, +,∗).

If the word set is new to you, you can think of it as a collection of unique items, much like a pallet of colors. Each color in the pallet is different, and you can have as many colors as you like. In the world of math, a set is similar: it’s a group of distinct elements, like numbers or objects, where each element is unique and there’s no particular order to them. Just like how our color pallet might have a variety of colors, a set can contain a variety of elements.

In linear algebra, when we talk about a vector space, we’re not just referring to a simple set like our pallet. Instead, we describe it using a special trio: (O, +,∗). Think of this trio as a more advanced version of our pallet, where we not only have a collection of colors (or elements) but also ways to mix and blend them to create new tones. Meaning if we blend two colors (addition) we will still have a color. Or if we add more of the same color, we still have a color (multiplication by a scalar). So if we define O such that elements are vectors:

O is a non-empty set whose elements are called vectors.
+ is a binary operation (vector addition) that takes two vectors from O and produces another vector in O.
∗ is an operation (scalar multiplication) that takes a scalar (from a field, typically ℝ or ℂ) and a vector from O and produces another vector in O.

We mentioned rules but what are those ?

if and are two vectors ∈ O then + must be in O.
λ ∈ ℝ and ∈ O then λ also needs to be in O.

Let’s not refer to what follows as rules; let’s call them axioms, and they must verify certain conditions to uphold the structure of a vector space. Axioms are fundamental principles that don’t require proof within their system but are essential for defining and maintaining the integrity of that system. In the case of vector spaces, these axioms provide the necessary framework to ensure that vectors interact in consistent and predictable ways. Each axiom must hold true for a set of vectors to be considered a vector space. This means that for any collection of vectors to qualify as a vector space, they must adhere to these axioms, ensuring operations like vector addition and scalar multiplication behave as expected:

Commutative property of addition:
$−→ −→ −→ −→ v + w = w + v$

Don’t worry there are a few more:

Associative property of addition:
$−→ −→ −→ −→ −→ −→ v + (w + t ) = ( v + w ) + t$
A zero vector exists:
$−→ −→ v + 0 = v$
An inverse element exists:
$−→ −→ −→ v + (− v) = 0$

Take two more to add to the collection, and these ones are for free!

Scalars can be distributed across the members of an addition:
$−→ −→ −→ −→ c( v + w ) = c v + c w$
Just as an element can be distributed to an addition of two scalars:
$−→ −→ −→ (c + d )v = c v + d v$

The last two!

The product of two scalars and an element is equivalent to one of the scalars being multiplied by the product of the other scalar and the element:
$(cd )−→v = c (d−→v )$
Multiplying an element by 1 just returns the same element:
$−→ −→ 1 ⋅ v = v$

Do you need to know these axioms to apply machine learning? Well, not really. We all take them for granted. The reason that I have included them is to try and spark some curiosity in your mind. We all take things for granted and fail to appreciate and understand the things that surround us. Have you ever stopped to think about what happens when you press a switch to turn a light bulb on? Years of development and studying had to take place for that object to be transformed into a color that illuminates your surroundings.

I feel that this is the right moment for an example, so let’s check out one of a vector space and another of a non-vector space. For a vector space, let’s consider ℝ². This is the space formed by all of the vectors with two dimensions, whose elements are real numbers. Firstly, we need to verify whether we will still end up with two-dimensional vectors with real entries after adding any two vectors. Then, we want to check that we obtain a new stretched or shrunk version of a vector that is still is in ℝ² after we multiply the vector by a scalar. As there is a need to generalize, let’s define two vectors −→ v and −→ w as being in ℝ². Let’s also define a scalar λ ∈ ℝ. If we multiply −→v by λ we have:

( ) −→ λ ⋅ v1 λ ⋅ v = ( λ ⋅ v2)

So, λ⋅ −→v has size two and both λ⋅v₁, λ⋅v₂ are real numbers because multiplying a real number by a real number results in a new real number. The only bit we are missing is the verification of what happens when we add −→ v with −→ w :

( ) v1 + w1 −→v + −→w = ( v + w ) 2 2

We have a vector of size two, and its elements belong to ℝ, as the addition of real numbers produces a real number, therefore ℝ² is a valid vector space. For the example of a non-valid vector space, consider the following, ℝ_≠(0,0)². This is the set of vectors with two dimensions excluding (0, 0)^T. This time we have:

( ) ( ) −→v = 1 and −→w = − 1 1 − 1

Adding these vectors results in (0, 0)^T , which is not part of ℝ_≠(0,0)².

Since we have spoken so much about ℝ², what would be really helpful is if there was a way to represent all of the vectors belonging to such a space. And, as luck would have it, there is such a concept in linear algebra called linear combination; this mechanism allows the derivation of new vectors via a combination of others.

The term linear suggests that there are no curves, just lines, planes, or hyper-planes, depending on the dimensions that we are working in. Here we are working with two dimensions, and a linear combination can be, for example:

( ) ( ) 1 0 α ⋅ 0 + β ⋅ 1 where α, β ∈ ℝ

Say that we name (1, 0)^T as −→ i and the vector with coordinates (0, 1)^T as −→ j . Let’s plot these vectors alongside the vector, −→v :

−→−→−→ xy−123−123ijv11

Figure 3.14: A vector as a linear combination.

The vector −→ v has for coordinates (2, 3)^T, which means that if we stretch −→ i by two units and then sum it to a three units stretched version of −→ j , the result will be equal to . Let’s call −→ ∗ i to the stretched version of and −→∗ j to the stretched version of . Algebraically we can represent −→ v as:

( ) ( ) 1 0 −→ ( ) ( ) v = 2 ⋅ 0 + 3 ⋅ 1

Which is the same as:

−→ −→ −→v = 2 ⋅ i + 3 ⋅ j

−→−→−→ −→ xy−234−234iij∗∗∗11+ j∗

Figure 3.15: A new representation of −→v

as a linear combination.

If we now replace the scalars two and three with two variables, which we’ll call α and β, where both of them are in ℝ, we get:

−→ −→ α ⋅ i + β ⋅ j

(3.4)

We can display all the vectors of the vector space ℝ² using equation 3.4. Let’s think about this affirmation for a second and see if it makes sense. If I have the entire set of real numbers assigned to the scalars α and β, it means that if I add up the scaled version of −→ i and −→ j , I can get any vector within ℝ². The vectors and have a particular property that is important to mention; they are linear independent. What this means is that you can’t get to via and vice versa. Mathematically this is defined by the following equation:

−→ −→ −→ c1 ⋅ v1 + c2 ⋅v3 + ...+ cn ⋅ vn = 0

(3.5)

In the equation 3.5, the factors c₁,c₂,…,c_n are scalars or real numbers. The v′s are a set of vectors that belong to the space and are linearly independent if, and only if, the values for the c′s that satisfy that equality are 0. Let’s verify if 3.4 satisfies this property:

( ) ( ) 1 0 ( ) ( ) α ⋅ 0 + β ⋅ 1 = 0

The only way for the equality to be true is if both α and β are equal to zero. Therefore, −→ i and −→ j are linearly independent. So, if the condition for linear independence is that the scalar values represented by the c′s have to be zero, then the opposite, meaning that at least one of them is not equal to zero, must mean that the vectors are linearly dependent, for example:

−→ −→ c1 ⋅v1 = − c2 ⋅ v2

Now, say that instead of (1, 0)^T and (0, 1)^T we have −→ w = (1, 1)^T and −→ z = (2, 2)^T:

−→−→ xy−1234−1234wz11

Figure 3.16: The showcase of linearly dependent vectors.

If we define a linear combination of these two vectors, this is what it will look like:

( ) ( ) 1 2 α ⋅ + β ⋅ 1 2

(3.6)

For any values of α and β, all of the resultant vectors from this linear combination 3.6 will land on the same line. This happens because −→ w and −→z are not linearly independent. So, we can get to −→w by −→z and vice versa:

−→ −→ z = 2 ⋅w

(3.7)

What we can observe from equation 3.6 is that we are not able to represent all of the vectors in the space using the two vectors, −→z and −→ w :

xy−1234−1234−→z−→w 11

Figure 3.17: A line formed by the linearly dependent vectors.

Another thing we can learn from this experiment is the concept of span; the continuing black line is an example of a span. All of the vectors that result from a linear combination define the span. For instance, in the case of −→i and −→j , the span is the entire vector space because we can get all the vectors within the vector space with a linear combination of these vectors, whereas with −→ z and −→ w , the span is a line. With this, we have arrived at the definition of a basis; for a set of vectors to be considered a basis of a vector space, these vectors need to be linearly independent, and their span has to be equal to the entire vector space, therefore −→ i and −→ j form a basis of ℝ². A vector space can have more than one basis, and ℝ² is one example of a space that contains many basis. When I first read this in a book, I was more confused than a horse riding a human. Why is there a need for more than one basis? I always felt tall. When frequenting bars, my shoulders were usually above the same pieces of anatomy of most people in my surroundings. One day, I went to the Netherlands, and boy oh boy, I felt short. I could see shoulders everywhere! My height had not changed, but my perspective had. You can think of a basis in the same way, perspectives from which we observe the same vector in different ways. Let’s define three vectors, two to form a basis, which will be −→ i = (1, 0)^T and −→ j = (0, 1)^T, the standard basis. And let’s consider another vector so we can understand what happens to it when the basis is changed, so let’s put the vector −→ v = (2, 3)^T back to work:

−→−→−→ ijv

Figure 3.18: The vector −→ v

from the perspective of the standard basis.

The grids represent our perspective or the basis, which is the way we observe −→ v on the basis formed by −→ i and −→ j . If we wish to write −→v via a linear combination, we can stretch the coordinate x by two units and the second coordinate, y, will be scaled by three units:

−→ −→ −→ v = 2 ⋅ i + 3 ⋅ j

Cool, more of the same stuff, a vector on an x,y axes where x is perpendicular to y. Say that we derive a new basis, a set of two linearly independent vectors whose span is the vector space, for example, −→ w = (1, 0)^T and −→ z = (1, 1)^T. These vectors are no longer perpendicular. The grid in the previous plot will change, and, consequently, so will the perspective from which we observe −→v :

−→−→−→ wzv

Figure 3.19: The vector −→ v

from a perspective of a different basis.

If we wish to calculate the new coordinates of −→ v using this new basis, we can once again make use of a linear combination:

−→v = v∗ ⋅ −→w + v ∗⋅ −→z 1 2

Where, v₁^∗ and v₂^∗ are the coordinates of −→v in the new basis. That expression becomes:

( ) ( ) ( ) 2 1 1 = v∗1 ⋅ + v∗2 ⋅ 3 0 1

This will result in two equations:

∗ ∗ 2 = v1 + v2

v∗ = 3 2

By replacing the value of v₂^∗ in the first equation we get that the coordinates of −→ v in the new basis formed by −→ w and −→ z are (−1, 3)^T. Understanding both the concept of a basis and the result of changing it is fundamental. As we advance, these manipulations will be a recurrent theme, and not only will we change the basis inside the same space, but we will also change spaces. Techniques like this will be useful because you can find properties of vectors or data using a different basis or spaces, which allows for faster computation or even better results when dealing with machine learning models.

For example, say that we wish to predict the price of a house, and our dataset consists of two measurements: the number of bedrooms and the number of bathrooms. In this context, the vector −→ i = (1, 0)^T will point in the directions where the number of bedrooms increases, whereas the number of bathrooms follows the orientation of the vector −→ j = (0, 1)^T. Suppose now that, after looking into the data, we noticed that houses with more rooms in total tend to have higher prices. Another trend we might have captured was that when the number of bathrooms is the same or close to the number of bedrooms, the higher price phenomenon is also present. Given this scenario, we can use a new basis to get a different perspective on the data, one that will allow us to understand those trends better. I have an idea, what if we defined −→ i∗ = (1, 1)^T and −→ j ∗ = (1,−1)^T as the new basis? Let’s think about this one for a second. The vector will represent the total number of rooms. On the other hand, −→ j∗ displays the difference in number between bedrooms and bathrooms. So, in this new basis, the house’s features are expressed not in terms of the absolute numbers of bedrooms and bathrooms but in terms of its total number of rooms (the first basis vector) and how balanced the number of bedrooms and bathrooms are (the second basis vector).

Should we change something? What about a basis? Sure thing! Say that we have the vector −→w defined as such:

( ) −→ 3 w = 2

This vector represents a house that is somewhat balanced in terms of rooms. It has three bedrooms and two bathrooms. Let’s check it from a new perspective, the one described by the new basis, −→∗ i and −→ ∗ j :

( ) ( ) ( ) 3 ∗ 1 ∗ 1 = w 1 ⋅ + w 2 ⋅ 2 1 − 1

OK, so we know that 3 = w₁^∗ + w₂^∗ and 2 = w₁^∗− w₂^∗ meaning that:

∗ ∗ w 2 = 3 − w 1

Therefore:

5 2 = w ∗− (3 − w ∗) ⇒ w ∗ = -- 1 1 1 2

So:

∗ 1- w 2 = 2

The vector −→ w ∗ = ( 5 2 , 1 2 )^T represents the same house but in different terms. The first component is associated with the vector −→ i∗ = (1, 1)^T, representing a direction in which the number of bedrooms and bathrooms increases equally. So, a value of 5 2 in this direction suggests that the house has a somewhat balanced distribution of bedrooms and bathrooms. The second component is associated with the other vector that constitutes the new basis, −→ j ∗ = (1,−1)^T. Here, suggests that the house has more bedrooms than bathrooms by half a room’s worth. This change in basis transformed the house’s representation that focused on the raw number of bedrooms and bathrooms, to the new basis, where attention defers to the balance and imbalance of the number of rooms. As a result, it’s a valuable technique for revealing different aspects of the data or preparing it for further analysis or manipulation. For example, it might be easier to analyse or predict house prices regarding the balance and imbalance of rooms rather than the raw numbers of bedrooms and bathrooms. A great example of an algorithm that uses such a technique is the principal component analysis, which we will cover in the last chapter.

Needless to say, there is another mathematical way to perform these transformations. For this purpose, we will be making use of something that is probably familiar to you, matrices.